現在、こちらのアーカイブ情報は過去の情報となっております。取扱いにはくれぐれもご注意ください。
(平成23年7月31日現在)
はじめに-
デリバティブ関連のバリュエーションを理解するためには、確率統計論と合わせて、微分・積分についてのある程度の理解が必要になります。微分・積分は、確率統計と同様にすべてを理解しようとすると多大な労力がかかるものとなるため、バリュエーションに必要なエッセンス部分のみについて解説していきます。今までと同様、数学的厳密性にはあまり拘らず解説をすすめていきます。
1-1.微分とは・積分とは
「微分する」というと、イメージ的に計算方法を思い浮かべる人が多いと思いますが、言葉として定義するとどうでしょうか。おそらく、「導関数を求めること」や「微分係数を求めること」と説明されることが多いかと思います。その説明でも当然間違いではないのですが、ここでは、あえて言葉のとおり「微小に分けること」という意味で説明していこうと思います。
「微分する」というのは、漢字からも理解できるように、「微小に分けること」に他なりません。例えば、次のような2次関数があったとしましょう。
この関数を以下のとおり、分解していきます。
これをさらに「微小に分けて」いきます。
このとき、この「dx」と「dy」を出すことこそが「微分する」ということです。
そして、ある値における、このときの傾き(変化率=xが増加したときのyの増加率)を表現したものが「微分係数」です。
さらに、この「dx」と「dy」の関係を表したものが「導関数」と言えます。
逆に、積分とは、「分けたものを積みあげること」です。微分で、微小に分けたものを足していけば、積分になるわけです。誤解を恐れずに簡単に表現すれば、「積分は足し算」に他なりません。積分は、一般的に原始関数を求める場合を「不定積分」といい、面積を求める場合に「定積分」といいます。
積分は、次のようなイメージで直感的に理解できると思います。
微分されたもの(つまり、導関数)を積分するということは、「微小に分けたもの」を足してあげていくことですから、微分前の関数へと戻されます。このため、元の関数なので、積分で求められる関数を「原始関数」を呼ばれます。
また、積分は原始関数を導くという特徴以外に、次のように関数下の面積部分を求めるときにも利用でき、これが実務的(実社会的)に非常に都合がよいものです。例えば、ファイナンスでは、確率密度関数が利用されています。正規分布を積分することで、ある値が発生する正規分布上の確率を求めることができるのです。正規分布の確率密度関数は次のように表現できます。
なお、上記で利用したように、積分記号「∫」は、加算記号「Σ」と同様に考えればよいかと思います。「Σ」記号は離散型(数字がとびとびとなっている)の場合に足し上げていく記号であるのに対し、「∫」記号は連続型の場合に足上げていく記号だと理解すればわかりやすいかと思います。
1-2.高階導関数と偏微分
さて、もとの関数を微分することで、導関数を求めることができましたが、この導関数をさらに微分することができます。導関数をさらに微分してもとめられる導関数を「高階導関数」といいます。2回微分することで求められた導関数を「2階導関数」といい、3回微分したものを「3階導関数」と呼びます。
この高階導関数は、様々な数学的場面で利用されますが、経済学やファイナンスでよく利用されるものは、関数の凸関数性を議論する場面です。「関数が凸」というのは、次のような関数です。
関数が凸であると、関数上の任意の2点を結ぶ直線は、その間のf(x)よりもすべて高い点にあるという特徴を持ちます。「凸」という概念は数学の集合論の概念になるので、非常に難しい話が伴いますが、直感的に話せば、次のような集合を考えてみるとわかりやすいと思います。
上記の集合では、任意の2点を結んだ直線はすべて同じ集合内に入ります。これは別の表現の仕方をすると、「任意の2点のどんな割合の組み合わせでも、また同じ集合の中にある」ということです。
例えば、消費可能集合Xの中に、Aという消費パターンとBという消費パターンが存在するとします。この消費パターンAと消費パターンBの割合に応じて、消費パターンAと消費パターンBの直線上に消費パターンCというものを作り出すことができます。ただ、この消費パターンCが、そもそも「消費可能」なものでなければならないため、消費パターンCもまた消費可能集合に入っている必要があります。
この「消費パターンCが消費可能集合に入っている」という前提を満たすために、「消費可能集合Xが凸集合である」という前提を置くのです。凸集合内の任意の2点を結ぶ直線上のすべての点が集合内に存在することが「凸集合」である定義であるため、消費可能集合Xが凸集合であれば、消費パターンCは消費可能集合Xに入っているといえます。
さて、話を戻すと、この凸性というのを求めるのが、2階導関数です。2階導関数が次のような場合には、もとの関数は凸関数といえます。
7-4.スチューデントのt分布
実際の統計の世界では、母分散![]() の値がわかっていないことがほとんどで、実際にわかるのは標本分散
の値がわかっていないことがほとんどで、実際にわかるのは標本分散![]() です。このため、母分散ではなく標本分散を用いていろいろと考える方法が重要となります。 標本平均
です。このため、母分散ではなく標本分散を用いていろいろと考える方法が重要となります。 標本平均![]() の標本分布は正規分布
の標本分布は正規分布![]() であり、その標準化されたZは標準正規分布に従うことになります。
であり、その標準化されたZは標準正規分布に従うことになります。
![]()
しかし、母分散がわかっていなければ、標準化Zの値を求めることはできません。ここで、わかっているのはあくまで標本分散です。このため、母分散の代わりに標本分散を用いた次の値を定義します。
![]()
このtは標準正規分布に従うわけではありません。標準正規分布に従うのは、あくまで母分散を用いたZであって、tが正規分布に従うわけではないのです。
では、このtはどういった確率分布になるでしょうか。tを次のように展開していきますと、標準正規分布と自由度n-1の![]() 分布の組合せであることがわかります。
分布の組合せであることがわかります。
【tの展開】
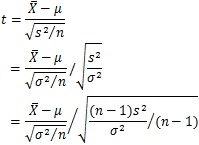
これをみれば、分子の部分が標準正規分布であり、分母の最初の部分が自由度n-1の![]() 分布となっていることがわかります。これから、tはいわゆる「t分布」に従うことといえます。
分布となっていることがわかります。これから、tはいわゆる「t分布」に従うことといえます。
【自由度kのt分布(スチューデントのt分布)】
二つの確率変数YとZが次の条件を満たす場合、確率変数tを次のように定義すると、この確率分布を自由度kのt分布、もしくはスチューデントのt分布といいます。なお、自由度kのt分布をt(k)と表現します。
条件1:Zは標準正規分布N(0,1)に従う。
条件2:Yは自由度kの![]() 分布に従う。
分布に従う。
条件3:ZとYは互いに独立である。
![]()
t分布の統計的な意味は、標本分布の数学的な精緻性を求めた点だと考えられます。標本数が十分に大きければ正規分布と結果が同じになるものの、それほどの標本の大きさがとれない場合などは正規分布に従うのではなくt分布に従うことになります。これによって数学的(計算的)な精緻さを与えることができると考えられるのです。なお、この分布を定義したのは実務家ゴセットで、ゴセットはこの論文を「スチューデント」という名前で発表したことから、「スチューデントのt分布」と名付けられています。
7-5.複数標本の分析のためのF分布
上項のt分布は、標本分布が1つの場合の用いられるものですが、ここでは標本分布が2つ用いられる場合のF分布について紹介します。
日本と中国の国民の所得平均だったり、男子と女子の賃金格差の問題であったり、2つの事象を比較して議論することはよく行われることです。このため、2つの母集団があり、異なる母集団をもつ2つの標本が抽出されて、その標本分布を比較する必要性が出てきます。このときに2つの標本分布の比較を「比」といいう形で行うのがF分布です。
F分布は次のように定義されます。
【F分布】
条件1:確立変数Xは自由度mの![]() 分布に従う。
分布に従う。
条件2:確率変数Yは自由度nの![]() 分布に従う。
分布に従う。
条件3:XとYは互いに独立である。
このとき、次のFは、自由度(m,n)のF分布といい、F(m,n)と表現します。
![]()
このF分布は、2つの標本の標本分散を比較するときにしばしば用いられます。標本分散は、の![]() (m-1)に従うことがわかっており、それぞれの標本分散は互いに独立であることから、標本分散の比はF分布に従うことがわかっています。
(m-1)に従うことがわかっており、それぞれの標本分散は互いに独立であることから、標本分散の比はF分布に従うことがわかっています。
【標本分散とF分布】
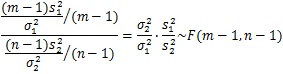
現在、こちらのアーカイブ情報は過去の情報となっております。取扱いにはくれぐれもご注意ください。

