現在、こちらのアーカイブ情報は過去の情報となっております。取扱いにはくれぐれもご注意ください。
(平成23年7月1日現在)
7-1.標本から母集団
ここでは、抽出されたサンプルから全体像を把握していく統計技術的な内容を解説していきます。
まず、調べたいと思っている全体像を統計学では母集団(population)とよんでいます。この母集団全体のことを知りたければ、母集団全体について調査をすればいいわけですが、現実として難しいことがしばしばあります。例えば、「日本人全体」を母集団とするならば、その母集団について調査することはコスト的に高くつき現実的ではありません。また、例えば、電池の使用可能時間を調べるのに、全部の電池を使って使用時間を調べてはまったく意味がありません(全部使い切ってしまっては販売することができないのだから当然)。
こうした現実的な問題から、母集団全体の特性を把握するために標本(sample)を抽出し、その標本に対して調査を実施し、母集団全体を推察していくという考えが芽生えてきます。これが統計的推察(statostocal inference)と呼ばれるものです。標本を抽出することを標本抽出(sampling)といいます。ここで、標本の数(大きさ)を標本の大きさ(sample size)といいます。
さて、母集団の特性を知ることが命題として、実際の統計的な課題は、その母集団がどのような分布に従っているのかをすでに知っているのか、それとも知らないのかによって大別することができます。前者をパラメトリック(parametric)といい、後者をノン・パラメトリック(non-parametric)といいます。
パラメトリックの場合、母集団がどういった分布に従っているかわかっているため、標本抽出による統計的推測は分布における定数ないしパラメータの確定作業といって過言ではありません。例えば、機械の寿命などを図る場合、指数分布に従うと経験則的にわかっていますが、指数分布の確率密度関数は、定数λによって表現されています。この定数λを標本によって推定することがまさに母集団への統計的推測に他なりません。また、代表的な確率分布である正規分布に母集団分布が従う場合、平均と分散を標本から求められれば、母集団の正規分布を推定することができます。
一方で、ノン・パラメトリックの場合には母集団分布が確定できていないため、平均、メディアン、モード、分散、歪度、尖度などの各種パラメータを求めて、それによって母集団分布を推定していく作業が行われるのです。
標本抽出の方法には、復元抽出(sampling with replacement)と非復元抽出(sampling without replacement)にわけることができます。復元抽出は、取り出したものを母集団にまた戻して抽出する場合のことで、非復元抽出は取り出したものを母集団に戻さないで抽出する場合です。ところで、標本抽出で重要なのは、抽出された標本が母集団を代表するような標本であり、それが選ばれる可能性が同程度あること、すなわち無作為(randam)に抽出されるという前提が重要です。
7-2.標本平均と標本分散
母集団を推定する際に重要なパラメータとなるのは、やはり平均と分散です。特に、母集団分布が正規分布に従うとすれば、平均と分散が求められれば、それだけで母集団が推定できてしまいます。
標本から算定された平均を標本平均(sample mean)、標本から算定された分散を標本分散(sample variance)といいます。なお、母集団の平均は母平均(population mean)、分散を母分散(population variance)といいます。
さて、標本平均は次のように表現できます。
【標本平均】
![]()
標本平均の期待値は母平均μと一致することが次のことから明らかです。
![]()
また、標本平均の分散は次のように求めることができます。
![]()
このため、n→∞とnが十分に大きい値となれば、分散はゼロとなり、母平均μに確率収束していくことがわかります。
さて、次に標本分散について考えてみましょう。
標本分散(正確には不偏分散)は次のように定義されます。
![]()
![]()
この標本分散を不偏分散(unbiased variance)といいます。nでなく、n-1で割ることで、上記のように標本分散の期待値が母分散に収束していくことになります(すなわち、過大でも過小でもない"不偏”)。なお、n-1でなく、nで割った標本分散だと、その期待値は母分散とは一致しません。
![]()
![]()
7-3.カイ二乗分布とは
さて、ここで標本分散の標本分布について考えてみましょう。例えば、測定誤差が正規分布N(0、![]() )に従うとすれば、次のように計算することができます。
)に従うとすれば、次のように計算することができます。
![]()
![]() であり、
であり、![]() の関係であるから、
の関係であるから、
![]()
ここで、測定誤差を二乗した値も確率変数であることに注目すると、この二乗した確率変数の和は次のように定義することができます。
【![]() 分布】
分布】
![]() が互いに独立で、標準正規分布N(0,1)に従う確率変数とすると、
が互いに独立で、標準正規分布N(0,1)に従う確率変数とすると、
![]()
の![]() が従う確率分布を自由度kの
が従う確率分布を自由度kの![]() 分布といいます。また、このとき、
分布といいます。また、このとき、![]() で表現します。
で表現します。
この結果から、不偏分散は、次のように自由度n-1の![]() 分布に従うといえます。
分布に従うといえます。
![]()
7-4.スチューデントのt分布
実際の統計の世界では、母分散![]() の値がわかっていないことがほとんどで、実際にわかるのは標本分散
の値がわかっていないことがほとんどで、実際にわかるのは標本分散![]() です。このため、母分散ではなく標本分散を用いていろいろと考える方法が重要となります。 標本平均
です。このため、母分散ではなく標本分散を用いていろいろと考える方法が重要となります。 標本平均![]() の標本分布は正規分布
の標本分布は正規分布![]() であり、その標準化されたZは標準正規分布に従うことになります。
であり、その標準化されたZは標準正規分布に従うことになります。
![]()
しかし、母分散がわかっていなければ、標準化Zの値を求めることはできません。ここで、わかっているのはあくまで標本分散です。このため、母分散の代わりに標本分散を用いた次の値を定義します。
![]()
このtは標準正規分布に従うわけではありません。標準正規分布に従うのは、あくまで母分散を用いたZであって、tが正規分布に従うわけではないのです。
では、このtはどういった確率分布になるでしょうか。tを次のように展開していきますと、標準正規分布と自由度n-1の![]() 分布の組合せであることがわかります。
分布の組合せであることがわかります。
【tの展開】
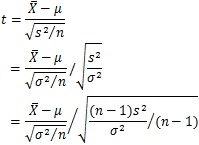
これをみれば、分子の部分が標準正規分布であり、分母の最初の部分が自由度n-1の![]() 分布となっていることがわかります。これから、tはいわゆる「t分布」に従うことといえます。
分布となっていることがわかります。これから、tはいわゆる「t分布」に従うことといえます。
【自由度kのt分布(スチューデントのt分布)】
二つの確率変数YとZが次の条件を満たす場合、確率変数tを次のように定義すると、この確率分布を自由度kのt分布、もしくはスチューデントのt分布といいます。なお、自由度kのt分布をt(k)と表現します。
条件1:Zは標準正規分布N(0,1)に従う。
条件2:Yは自由度kの![]() 分布に従う。
分布に従う。
条件3:ZとYは互いに独立である。
![]()
t分布の統計的な意味は、標本分布の数学的な精緻性を求めた点だと考えられます。標本数が十分に大きければ正規分布と結果が同じになるものの、それほどの標本の大きさがとれない場合などは正規分布に従うのではなくt分布に従うことになります。これによって数学的(計算的)な精緻さを与えることができると考えられるのです。なお、この分布を定義したのは実務家ゴセットで、ゴセットはこの論文を「スチューデント」という名前で発表したことから、「スチューデントのt分布」と名付けられています。
7-5.複数標本の分析のためのF分布
上項のt分布は、標本分布が1つの場合の用いられるものですが、ここでは標本分布が2つ用いられる場合のF分布について紹介します。
日本と中国の国民の所得平均だったり、男子と女子の賃金格差の問題であったり、2つの事象を比較して議論することはよく行われることです。このため、2つの母集団があり、異なる母集団をもつ2つの標本が抽出されて、その標本分布を比較する必要性が出てきます。このときに2つの標本分布の比較を「比」といいう形で行うのがF分布です。
F分布は次のように定義されます。
【F分布】
条件1:確立変数Xは自由度mの![]() 分布に従う。
分布に従う。
条件2:確率変数Yは自由度nの![]() 分布に従う。
分布に従う。
条件3:XとYは互いに独立である。
このとき、次のFは、自由度(m,n)のF分布といい、F(m,n)と表現します。
![]()
このF分布は、2つの標本の標本分散を比較するときにしばしば用いられます。標本分散は、の![]() (m-1)に従うことがわかっており、それぞれの標本分散は互いに独立であることから、標本分散の比はF分布に従うことがわかっています。
(m-1)に従うことがわかっており、それぞれの標本分散は互いに独立であることから、標本分散の比はF分布に従うことがわかっています。
【標本分散とF分布】
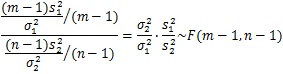
現在、こちらのアーカイブ情報は過去の情報となっております。取扱いにはくれぐれもご注意ください。

