２次元の確率分布、大数の法則と中心極限定理

（平成23年7月1日現在）

６－１．２次元における確率分布

　前項までは、１次元の確率分布について解説しましたが、ここでは２次元の確率分布について解説します。２次元の確率分布は、それぞれの確率変数が独立している場合もあれば、それぞれの確率変数が影響を受け合うことも考えられます。例えば、株式投資を考えた場合、株式Xと株式Yの間に何かしらの関係が存在するとした場合、株式Xの収益率の確率分布は株式Yの収益率の確率分布に影響を与えることになります。一方で、まったく影響を与えあわず、それぞれ独自に株価が動く場合もあります。

　２次元ないし多次元の確率分布等が議論されるのは、ファイナンスにおいてポートフォリオ概念を議論する場合です。ここでは、多変量解析の基礎となる２次元の確率解析について解説します。

　２次元確率変数（X,Y）について、それが同時に発生する確率を次のように定義します。これを離散型では同時確率分布（joint probability distribution）、連続型では同時確率密度関数（joint probability density function）といいます。

【離散型】

【連続型】

　連続型の場合は確率変数が区間となることから、集合Aの中で発生する確率分布と定義されます。また、この集合Aは、集合Sの部分集合として定義され、集合Sは確率分布が存在しうる集合で、確率論では標本空間（sample space）と呼ばれています。標本空間における累積確率分布は１となります。

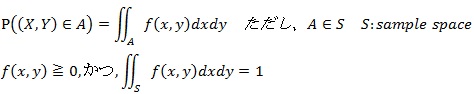
　また、同時確率分布から派生して、周辺確率分布（marginal proibability distribution）ないし周辺確率密度関数（marginal probability density function）を以下のように定義することができます。

【離散型】

【連続型】

６－２．共分散と独立、条件付確率分布とは

　互いの変数同士に何らかの関係がある場合の指標として利用されるのが、共分散（covariance）や相関係数（correlation coefficient）です。これは、すでに学習したものと違いはありません。共分散と相関係数を定義すると次のようになります。

【共分散】

【相関係数】

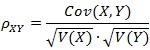
　さて、ここで、変数がそれぞれ独立（independent）しているとはどういうこでしょうか。それぞれが独立しているとは、同時確率分布が次の条件を満たすときです。

【それぞれ確率変数が独立であるための条件】

　上記の場合、確率変数は独立しているといえます。また、それぞれの確率変数が独立である場合、それぞれの確率変数の積の期待値は、次のように計算できます。

　この結果、互いに独立している場合、共分散（ないし相関係数）がゼロとなります。共分散（ないし相関係数）がゼロとなることを無相関（uncorrelation）といいます。互いに独立の場合は必ず無相関となりますが、無相関であるからといって必ずしも独立とは限りません。

　ところで、周辺確率分布と似た概念で条件付確率分布というものがあります。条件付確率は次のように定義されます。

【条件付確率】

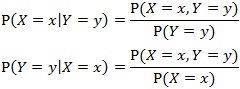
　この結果、条件付確率密度関数（conditional probability density function）は次のように定義されます。

【条件付確率密度関数】

　さて、再度、互いに独立の定義を確認してみよう。互いに独立の場合、次のように計算できます。

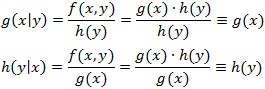
　上記のことからわかるように、互いに独立とは、他の変数に関係なく、自己の確率分布が決定することを意味しています。

６－３．確率変数の加法性

　２つの確率変数X,Yについて、２つを足したX+Yの期待値と分散は次のように計算することができます。これを確率変数の加法性といいます。

【期待値】

【分散】

（互いに独立）

（独立でない）

　さて、独立変数がｎ個になった場合はどうでしょうか。特に互いに独立している場合は次のようになります。

【期待値】

【分散】

　また、独立変数がすべて等しい場合は次のように計算できます。

【期待値】

【分散】

６－４．確率分布の再生性

　確率分布の再生性（reproduvtiveness）とは、同じ種類の確率分布に従っている確率変数であり、かつ、それぞれの確率分布が互いに独立していれば、その確率変数の和は、また同一種類の確率分布に従うことをいいます。

　例えば、正規分布に従う場合を数学的に表現すれば、次のように表現できます。

【正規分布の再生性】

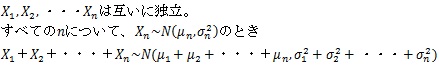
　再生的である確率分布は正規分布だけでなく、二項分布やポアソン分布、ガンマ分布なども再生的です。

　再生的であることは数学的にとても扱いが楽になる性質です。例えば、誤差項などは正規分布に従うと仮定して計算しますが、誤差項同士の和もまた正規分布に従うことになり、扱いが非常に楽なわけです。

６－５．大数の法則

　確率論における重要な定理として必ず挙げられるのが、大数の法則（law of large numbers）と次項で解説する中心極限定理（central limit theorem）です。

　大数の法則は、ベルヌーイ試行の回数が多くなると、観察された確率が理論的（数学的）な確率（つまり確率分布の値）に一致していくという法則です。すなわち、ベルヌーイ試行の回数が大きければ、確率分布上で求められる「真の値」に限りなく近づいていくことを意味しています。

　例えば、サイコロをふって１の目が出る確率を考えてみましょう。理論的に考えれば「１／６」と求めることができますが、サイコロを実際に６回ふってみても、必ずしも１の目が１回出るとは限りません。しかし、大数の法則は、ベルヌーイ試行回数が大きくなれば、観察された値が真の値と一致することを数学的に証明しているのです。

　大数の法則の意義は、標本における統計的推測をしても問題ないことを数学的に証明したことに他なりません。例えば、「日本の小学生のうち、数学好きな児童の確率」を求めたいとき、日本全国の小学生全員に数学が好きかどうかをアンケートすることなく、十分な人数の小学生にアンケートを実施して、それをもとに計算すれば、命題「日本の小学生のうち、数学好きな児童の確率」を求めることができるのです。

　さて、この大数の法則を、εを任意の正の定数、確率分布の平均をμ、実際に観察されたｎ個の値の平均をとすると、次のように表現できます。

【大数の法則】

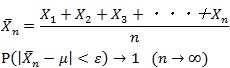
　これは、平均μから観測値がずれる確率（十分に小さい値εに収まる確率）を求めているもので、ｎ→∞となる場合には、確率１、すなわち100％の確率で収まるということを表現しています。

６－６．中心極限定理とは

　前項の大数の法則と合わせて、確率論の重要な定理の1つに中心極限定理です。

　中心極限定理とは、簡単に説明すると、どのような確率分布であっても、確率変数X1,X2,X3・・・Xnの和の確率分布の形状は、ｎが大きいと、大概に正規分布となるというものです。ここで重要なのは、「どんな確率分布であっても」確率変数の和の確率分布が大概に正規分布を作ってしまうというものです。

　これを数式で表現すると次のように表現できます。

【中心極限定理】

　上記の式は、N(0,1)に従うように標準化したものです。このため、μ＝０、σ＝１が正規分布の式に代入されています。

　繰り返しになりますが、中心極限定理の意義は、どのような確率分布であっても、ｎが十分に大きくなると正規分布に従う確率分布となるという点です。バリュエーションの実務では、バリュエーション計算における正規乱数の生成の際に、一様乱数から正規乱数を中心極限定理によって導きだす方法が利用されるケースがしばしば見受けられます。この理由は、最もポピュラーな計算ソフトであるマイクロソフト社のエクセルに一様乱数の値をかえすrand関数が実装されているため、一様乱数から中心極限定理を用いて正規乱数を導き出そうとしているのです（乱数生成については後述）。