現在、こちらのアーカイブ情報は過去の情報となっております。取扱いにはくれぐれもご注意ください。
(平成23年7月1日現在)
3-1.確率と確率変数
確率(probability)とは、事象の起こりやすさを定量的に示すものです。ファイナンスにおいても、将来どのような株価となるのか、どのような金利となるのかを現時点で知る者は結局は誰もいないし、知ることもできないから、「確率的にこうなるだろう」と予測するしかありません。例えば、「50%の確率で株価があがる」とか、「70%の確率で金利は下落する」などです。こうした確率的な視点から、株価ないし金利などを予測し、様々な金融商品の評価をすることができるのです。
さて、確率論を扱うために、まず基本的に知っておくべきものが、確率変数と確率分布の概念です。
各値に対してそれぞれ確率が与えられている変数が確率変数(random variable)です。例えば、サイコロの1から6までの目が確率変数です。
また、それぞれの確率変数に対応する確率、
![]()
をXの確率分布(probability distribution)といいます。サイコロで言えば、サイコロの1から6が確率変数で、その確率変数が出る可能性、すなわち、1の出る確率1/6、2の出る確率1/6・・・・6の出る確率1/6が確率分布となります。サイコロのように確率変数が離散的な場合、離散型(discrete type)の確率分布といいます。
確率分布の最大の特徴は、各確率変数の出る確率がゼロ以上であり、かつ、各確率変数の和が必ず1になることです。数式上で表現するとなれば、次のとおりです。
![]()
3-2.確率密度関数と累積分布関数
上記は離散型の確率分布です。次に、連続型の確率分布について考えます。
今、確率変数Xが次のような関数をとる場合、確率変数Xは連続型(continuous type)の確率分布をもつといいます。
![]()
また、すべてのxについて、次の条件を満たすものとする。
![]()
この関数fをXの確率密度関数(probability density function)といいます(単に密度関数ということもあります)。離散型でもそうであったように、連続型であっても各確率変数に対する確率はゼロ以上であり、各確率変数の確率の和(ここでは積分)は1となります。
ファイナンスでは、現実の株価は整数型しかとらないため離散型が適するものの、数学的な取扱いから連続型の確率密度関数を利用することがほとんどです。
なお、ある値以下の確率がどれぐらいかを求められるものとして、累積分布関数(cumulative distribution function)というものがあります。累積分布関数は次のように表現できます。
![]()
3-3.確率変数における期待値と分散
確率分布も度数分布(ヒストグラムなど)と同様、「分布」です。このため、代表値と散らばり具合で分布の形状を考える必要があります。
(A) 期待値
確率分布の代表値についても、平均、メディアン、モードが考えられます。
確率分布における平均を期待値(expectation)といいます。期待値は、確率変数を確率で加重平均したものです。期待値は次のように定義できます。
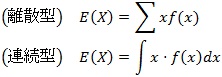
これは、Xがある関数であっても、同様に次のように定義することができます。
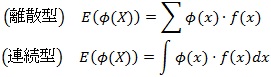
期待値について、次のような性質があります。計算過程は省略しますが、ファイナンスではよく利用される演算式です。
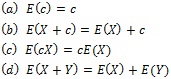
なお、確率分布の代表値にはモード(mode)とメディアン(median)も同様にあります。モードは、f(x)が最大値となるxであり、メディアンは、P(X≦x)=1/2となるxとなります。
(B) 分散と標準偏差
確率分布の場合でも、分布の形状を知るためには、代表値だけでなく、散らばり具合も知る必要があります。散らばり具合は、分散と標準偏差が用いられます。分散の定義は、統計の基礎で解説したように、平均偏差の二乗の平均で求められます。平均偏差の和は結局はゼロになるから、絶対値の和もしくは二乗の和を用いる必要があり、計算の簡便性から二乗和を用いて計算します。
期待値E(X)を表記の簡便性からμとして表すと、分散V(X)は次にように定義することができます。また、分散と標準偏差の関係から標準偏差D(X)についても次のように表現できます。
![]()
![]()
また、分散は次のような等式が成立し、計算が容易になるので、よく利用されます。
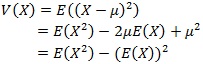
分散においても、期待値と同様に、次のような性質があります。計算過程は省略しますが、期待値と同様、ファイナンスではよく利用されます。
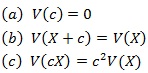
(C) 標準化
確率分布においても標準化があります。標準化は、期待値0、分散(標準偏差)1にすることです。
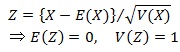
3-4.歪度と尖度、モーメント
(A) 歪度と尖度
代表値と標準偏差を知っていれば、確率分布の特徴をある程度知ることはできるものの、確率分布そのものを決定することはできません。左右対称性がどれぐらい歪んでいるか、確率分布の峰の部分が尖っているのか、それとも平らなのか、そのような情報は代表値と標準偏差だけから知ることはできません。
このとき、歪み具合を知るのが歪度(わいど)(skewness)、峰の部分の尖り具合を知るのが尖度(せんど)(kurtosis)といいます。
歪度と尖度は、次のように定義されています。
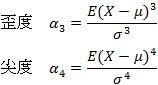
もしくは、歪度と尖度はしばしば次のように計算されます。
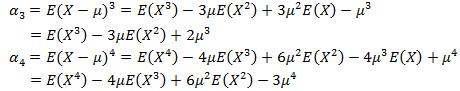
これは、次で説明するモーメント母関数を用いると、Xの高次元の期待値を簡単に計算することができるため、結果として容易に歪度と尖度を求めることができるからです。
なお、正規分布の尖度が3になることから、この尖度3を基準に比較することがしばしばあります。尖度が3より大きければ正規分布より尖っていることになります。
(B) モーメント
上記の歪度や尖度だけでも、確率分布そのものを確定することができません。しかし、歪度と尖度の計算式をみると、期待値の周りで次数をあげていき、その値を計算していけば、特定の確率分布に決定できるのではないかと予想できます。
ここで、次の式を期待値のまわりのr次のモーメント(moment)と定義できます。
![]()
また、次の式は標準化モーメントと言われています。歪度や尖度もこれにより求められます。
![]()
なお、すべての次数のモーメントを生成するモーメント母関数を次のように定義します。これは、ファイナンスではあまり利用しませんが、知っておくと確率分布の計算が容易になることがあります。
![]()
なお、これを計算すると次のように計算できます。
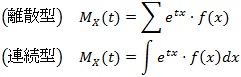
現在、こちらのアーカイブ情報は過去の情報となっております。取扱いにはくれぐれもご注意ください。

