オプションとは

（平成23年７月１日現在）

３－１．オプションとは

　オプション取引（option）は、「決められた時期」（もしくは決められた一定期間）に「決められた価格」で、「決められた数量」を購入するもしくは売却する権利をいいます。

　「一定の時期（その　日だけ）」のみ権利行使できるものをヨーロピアン・タイプ（European type）といい、「一定の期間（例：平成22年１月1日から平成23年12月31日まで）」で権利行使できるものをアメリカン・タイプ（American type）といいます。権利を保有している側をロング・ポジションといい、権利を売却している側をショート・ポジションといいます。また、「購入する権利」をコール（call）といい、「売却する権利」をプット（put）と言います。

　オプションは「権利」であり、「義務」ではありません。このため、これを行使するかどうかは保有者の自由であり、行使「しなければならない」ということはありません。これが他のデリバティブ取引と大きく相違する点です。先物取引やスワップ取引は「義務」であって「権利」ではありません。このため、必ず契約条件に従った履行が必要になります。なお、オプションを売却した側は、オプション保有者が権利行使したならばそれに応じなければなりません。 　

　さて、オプション取引のペイオフ関係はどのようになっているでしょうか。例えば、１年後に１株120円で購入できるコール・オプションを考えてみましょう。オプションのペイオフは、１年後の株価に依存することになります。なお、このときの「120円」を権利行使価格（strike price）といいます。

【１年後の株価が100円の場合】

１年後の株価が100円の場合、100円で株を購入できるので、わざわざオプションを行使しなくてもよいので、オプションのペイオフはゼロとなる。

【１年後の株価が140円の場合】

１年後の株価が140円の場合、オプションを行使すると120円で１株購入できるので、120円で株価を購入し直ちに売却すれば20円（＝140－120）のペイオフを発生します。

　上記の結果から、このコール・オプションのペイオフを図で表すと以下のようになります。

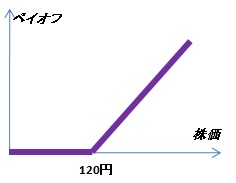
　この図からわかるように、オプションのペイオフは権利行使価格を境にして、ペイオフがゼロの状態であるものと、ペイオフが角度45度の直線になるものとの２つに分けられます。数学的な表現をすれば、これを「非線形性」といいます。つまり一直線では表現できないということです。この非線形性という特徴によって、バリュエーションでは数学的な工夫が必要となります（後述）。

３－２．オプションにおけるバリュエーションの基本

　上項でみたとおり、オプションのペイオフは将来の株価に依存するため、将来株価を算定する必要があります。すなわち、将来の株価がいくらになるかを予想する必要があるのです。このため、「確率論」という数学的技術が必要となり、他の金融商品とは少し毛色の違ったものが登場することになります。そして、この確率論こそがバリュエーションの理解を難しくさせるものであり、現代ファイナンスへの抵抗感を高める要因となっています。また、後述するブラック＝ショールズモデルにおいて、偏微分方程式が登場することから更に数学的な難易度を高めていくことになります。本シリーズでは、ある程度の数学的な意味を解説するものの、その精緻さ（証明）を与えることなく、オプションのバリュエーション方法について解説していきたいと思います。IFRSをはじめ、公正価値会計へとすすんでいくことが予想される中で、オプション的な条件が付されている金融商品（いわゆる組込デリバティブ）を無意識のうちに保有していることもあり、バリュエーション方法を理解しておくことはファイナンス担当者としては必須の「技術」だと考えられます。

　オプションにおけるバリュエーション方法は、大きく分けて３つの方法が利用されています。

(A)　ブラック＝ショールズモデル

　ブラック＝ショールズモデル（BSモデル）は、フィッシャー・ブラック（Fischer Black）とマイロン・ショールズ（Myron Scholes）が共同で発表し、ロバート・マートン（Robert C. Merton）がその証明を与えたオプション価格の有名な評価モデルです。　BSモデルは、ヨーロピアン・タイプのオプション価格を算定するモデルです。関数化・一般化されているため、計算が非常に楽で、かつ、誰が計算しても同じ結果になるというメリットがあります。ただし、ヨーロピアン・タイプの評価モデルであるため、アメリカン・タイプの評価には適さないし、複雑な条件が付されたオプションを評価することはできません。

(B)　格子モデル

　格子モデルは数学的な複雑性は特になく、その内容を理解することは非常に簡単です。また、BSモデルと異なりアメリカン・タイプの計算もできるし、ある程度の条件であれば条件付きのオプションを評価することができます。ただし、実務的には計算プログラムを組成する能力が別途必要となり、自社内で計算することは難しいように思われます。また、BSモデルと比べれば計算時間もある程度かかります。最近はパソコンの処理能力が高くなっているためそれほど負担感はありませんが、場合によっては計算結果が出るまで1時間ぐらいはかかるときもあります。このため、即時に計算結果を出してシミュレーションをすることができないことも考えられます。格子モデルは、二項モデル、三項モデル、多項モデルがありますが、実務的には収束性の問題などから二項モデルを採用することが多いと思われます。

(C)　モンテカルロ・シミュレーション　

　モンテカルロ・シミュレーションは将来株価についてシミュレーションを実施し、そのシミュレーション結果によってオプション価格を算定する方法です。モンテカルロ・シミュレーションは様々な条件が付されたオプションのバリュエーションに対応することができるという長所があります。しかし、実務的には、二項モデルと同様、計算プログラムを組成する能力が必要になります。また、計算過程が複雑であることから二項モデル以上に計算時間がかかり、基本的に数時間を要します。計算時間はシミュレーション回数に依存しますが、シミュレーション回数が少ないと適正な価格にたどりつかなくなる可能性があるため、通常は十万回程度のシミュレーションを実施します。このため、よっぽど処理能力の高いコンピュータを利用しない限り、数時間はかかると考えられます。

　さらに、計算結果はシミュレーション結果に依存するため、毎回の計算結果が異なるという最大のデメリットがあります。これは計算結果の検証が難しいということも意味しています。 　

　本シリーズでは、オプションのバリュエーション方法について、パラメータをはじめ順次解説していきます。繰り返しになりますが、数学的精緻さについてはあまり言及せず、各種モデルの基本的概念について解説していきます。なお、数学の基礎は、補論で解説している「統計学」や「微積分」を参考にしてください。