現在、こちらのアーカイブ情報は過去の情報となっております。取扱いにはくれぐれもご注意ください。
(平成23年7月1日現在)
4-1.債券のリスクとは
債券のリスクは、以下のようなリスクがあります。
| リスク | 内 容 |
| 金利リスク | 市場金利が変動することで債券価格が変動するリスク。 |
| 再投資リスク | 利付債において、受取った利息を再投資する際の利子率が不確実であるリスク。再投資利子率が不確実であると、将来価値が確定できない。 |
| 信用リスク | 利払い・元本返済が予定どおりに支払われない貸倒リスク。 |
| 流動性リスク | 債券の換金性の容易さに係るリスク。一般的にマーケットが存在しないと流動性リスクが高まる。 |
| 期限前償還リスク | 期限前償還条項が付されている場合の期限前償還リスク。すなわち、予定しているキャッシュ・フローが変動するリスクのことである。 |
債券投資は、マーケットにおける金利変動に大きな影響を受けるため、金利リスク等の市場リスクの管理が重要視されます。ただし、事業債といった事業会社の社債へ投資を行う際には信用リスクが発生するため、発行体の信用リスクの管理も重要視されます。
まずは、金利リスクの部分について、どのような管理手法があるのか解説します。
4-2.金利と債券価格の関係
債券の金利リスク管理は、金利の変動により、債券価格がどのように変動するのかを把握・管理することに他なりません。債券価格と金利の関係は、以下のとおりトレード・オフの関係にあります。
- 金利が上昇 ⇒ 債券価格は下落
- 金利が下落 ⇒ 債券価格は上昇
このことは、債券価格を求める式から明らかです。債券価格式の分母に金利があり、金利が上昇すれば分母が大きくなるため債券価格は下落するし、金利が減少すれば分母が小さくなるため債券価格は上昇します。
口述的な説明をすれば、固定利付債のクーポン・レートと現状の金利の関係から理解することもできます。例えば、クーポン・レートが3%の固定利付債を考えてみましょう。固定利付債のクーポン・レートは、市場金利がどのように変動しても変化することはありません。市場金利が3%から4%に変化したとします。すると、市場では4%の利回りが期待できる投資状況にあるにもかかわらず、当該固定利付債は3%であるため、この固定利付債に投資する価値はありません。このため、債券は売られていきます。この結果、債券価格は下落するのです。金利が下落した場合には、その逆のことが言えます。
さて、金利と債券価格の関係を理解する上で、もう1つ重要なことは、「債券の満期日までの期間」です。例えば、クーポン・レート3%の固定利付債が、最終利回りが1%上下した場合の変化率を示したものを示すと次のとおりです。
| 年限 | 最終利回り4% | 最終利回り2% |
|
1年 |
99.03円(△0.97%) | 100.98円(+0.98%) |
| 5年 | 95.55円(△4.45%) | 104.71円(+4.71%) |
| 10年 | 91.89円(△8.11%) | 108.98円(+8.98%) |
これから明らかなように、満期までの残存期間が長い債券の方が金利の変化に影響を受けやすいと言えます。期間が長い方が再投資リスクが高まるため、債券価格の変化率は高まると考えられます。
4-3.金利変化に関する感応度計算(修正デュレーションの計算)
上項で説明したような債券の金利リスクを図る指標として実務的によく利用されているのが、デュレーション(duration)です。本項では、デュレーションについて解説していきます。
金利変化と債券価格の変化の関係について分析したものが、修正デュレーション(modified duration)と呼ばれるものです。修正デュレーションは、金利変化に対する債券価格の感応度を示したもので、債券価格変化率が金利変化率の何倍かを表す尺度です。なお、ここでいう金利には、「最終利回り」を用いて、修正デュレーションを解説します。これを発展させるとスポット・レートを用いて分析しますが、スポット・レートだと変数が複数になり、数学上の取扱いが難しくなるので、まずは最終利回りという1つの変数だけを用いて分析します。
まず、債券価格Pと最終利回りrには、次のような関数P(r)が成立しています。
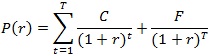
ここで、C:クーポン・レート、F:額面、t:期間(T期間まで)
次に、金利変化に対する債券価格の感応度を数式で表現すると次のようになります。
![]()
ここで、修正デュレーションは、この場合のΔr→0としたときの値となります。
![]()
つまり、修正デュレーションは、債券価格関数を最終利回りで微分したものを債券価格で割った値として定義されます。
rで微分したものは次のとおりです。
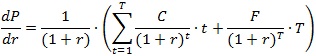
このため、修正デュレーションは次のように表現できます。
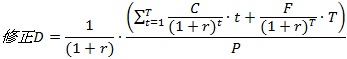
4-4.回収期間における期間分析(マコーレー・デュレーション)
さて、上記の修正デュレーションの丸で囲っている部分は、何を意味しているか考えてみます。

この部分は、各年数について、各年度の投資回収額の現在価値で加重平均したものです。つまり、平均残存年数を意味します。
平均残存年数が長い債券の方が、この囲っている部分が大きくなり、修正デュレーション、すなわち金利変化率に対する債券価格変化率の感応度は高くなることを示しています。この平均残存年数の部分を、最初の考案者マコーレーの名前をとって、マコーレー・デュレーション(Macaulay duration)といいます。
マコーレー・デュレーションは、単一の債券を管理するというよりは、債券ポートフォリオの金利リスク管理の債の指標としての方が理解しやすいかもしれません。
例えば、額面Cもしくは額面Fで期間が各年度となる割引債に投資するポートフォリオを考えてみましょう。期間t年の額面Cの割引債の価格は ![]() と表現できます。このことから、この投資ポートフォリオの投資額は合計するとPとなります。すなわち、マコーレー・デュレーションは、債券ポートフォリオの平均残存年数に他なりません。
と表現できます。このことから、この投資ポートフォリオの投資額は合計するとPとなります。すなわち、マコーレー・デュレーションは、債券ポートフォリオの平均残存年数に他なりません。
4-4.コンベクシティによる管理
さて、債券のリスク管理では、デュレーションだけでなく、コンベクシティ(convexity)という指標も用いて行われるのが一般的です。修正デュレーションだけでは、金利変化リスクを完全に表現できていないからです。
修正デュレーションは、金利が微小変化したときの債券価格の変化率を表しているものであり、金利が十分に変化した場合の変化率を表しているわけではありません。このため、修正デュレーションが同じであっても、金利が十分に変化した場合の債券価格の変化率が等しいとは限りません。金利変化が大きいと考えられる場合には、修正デュレーションだけでは十分な管理ができないのです。
そこで、修正デュレーションを補足するものとしてコンベクシティが利用されます。コンベクシティは、「金利変化率が変化した場合の債券価格変化率の変化率」として定義することができます。例えば、債券Aのコンベクシティが80、債券Bのコンベクシティが100とすると、債券Bの方が、金利の変化が大きいと予想される市場では有利となります。
コンベクシティを数式で表現すると次のとおりです。
![]()
上記の式を見てわかるように、コンベクシティは修正デュレーションについて最終利回りrでもう1階微分したものに該当します。別の言い方をすれば、債券価格を最終利回りで2階微分したものをPで割ったものとなります。
さて、債券価格の最終利回りrの2階微分は次のように計算できます。
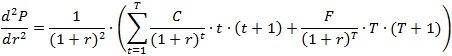
このため、コンベクシティは、次のとおり定義することができます。
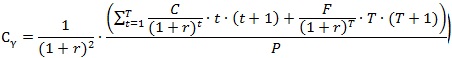
一般的に、市場における金利変化は数学的には「十分な変化」と言えるので、債券投資を考える上ではコンベクシティが大きい債券(ないし債券ポートフォリオ)が好まれます。この「コンベクシティが大きき方が選好される」ことによる債券価格の上昇(すなわち、利回りの低下)をコンベクシティ・コスト(convexity cost)といいます。金利変化が大きい場合(すなわち、金利ボラティリティが高い場合)に、コンベクシティ・コストは高まります。この結果、マーケットにおいて金利ボラティリティが高い場合には、イールド・カーブが長期にかけて低下していく(すなわち、曲率が高くなる)現象が発生します。
【補論】 テイラー展開とコンベクシティ
債券価格関数Pにおいて、債券価格の変化ΔPは、債券の最終利回りの瞬間的な変化Δrについて、次のようにテイラー展開が可能となります。
![]()
この展開式の両辺をPで割り、第2項で近似するとすると次のように計算することができます。
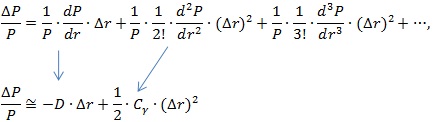
この結果から、例えば、金利変化率が十分に大きい場合に、第2項のコンベクシティの値は無視できないものとなり、金利変化率が大きい場合にコンベクシティが影響することが数式から読み取れます。逆に、金利変化率が十分に小さい場合には、第2項の値は十分に小さくなりコンベクシティの影響はほとんど受けないことがわかります。
4-5.パラレルシフトとノンパラレルシフト
イールド・カーブの変化には、パラレルシフト(parallel shift)とノンパラレルシフト(non-parallel shift)という2つの場合が想定できます。
パラレルシフトは、その名のとおり、パラレル=平行に移動することで次のようなものです。
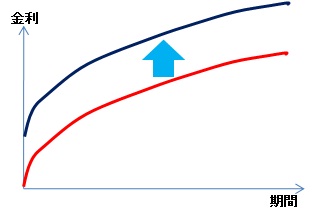
一方で、ノンパラレルシフトとは、パラレルではないシフトのことで、次のような変化の場合が該当します。
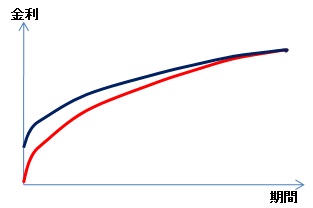
パラレルシフトは、イールド・カーブ全体の平行移動であるため、最終利回りという単一の変数だけ用いて分析しても特に大きな問題はありません。
しかし、ある特定のスポット・レートのみが変動し、上記図のようなイールドカーブの変化を起こすノンパラレルシフトが発生したとすれば、あるスポット・レート部分の変化率について管理する必要があり、修正デュレーションやコンベクシティの管理にも限界が生じてきます。
こうしたノンパラレルシフトの管理は、最終利回りのような1つの変数だけでなく、「各期間のレート」という複数の変数を用いる必要がありあす。ノンパラレルシフトは、あるスポット・レートの変化に対するものを分析するため、あるスポット・レートで債券価格関数を偏微分してデュレーション等を求める方法で行われます。このため数学的にはより高度な処理が必要となり、ここでは詳しい解説を省きます。
現在、こちらのアーカイブ情報は過去の情報となっております。取扱いにはくれぐれもご注意ください。

