離散型の確率分布

（平成23年7月1日現在）

４－１．二項分布

　例えば、株価の「上昇」と「下落」という２種類の結果が生じる観察を行い、それらの確率がそれぞれ、上昇＝ｐ、下落＝１－ｐとします。同じ条件で、かつ、独立してｎ回観察し（これをベルヌーイ試行（Bernoulli trials）といいます）、上昇がｘ回、下落がn-x回生じたとすると、その確率は、次のようにあらわすことができます。

　もしくは、

　この確率分布を二項分布（binomial distribution）といいます。この確率分布の期待値（平均）と分散は次のように計算できます。

　二項分布は、最も基本的な確率分布であり、よく利用されるものです。ファイナンスにおいても、オプションのバリュエーションにおける二項モデルの基礎的概念を与えるものです。

　なお、ベルヌーイ試行は、次の３つの条件を満たしたものです。

(1)　各回の試行結果は、事象かその余事象のいずれかである（二値性）

(2)　各回の試行において事象Aが起こる確率P(A)＝ｐは一定である（定常性）

(3)　各回の試行はお互いに影響を与えない（独立性）

【二項分布の期待値の計算過程】

　二項分布の期待値の計算過程を示すと以下のとおりです。

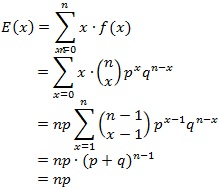
【二項分布の分散の計算過程】

　二項分布の分散の計算過程を示すと以下のとおりです。

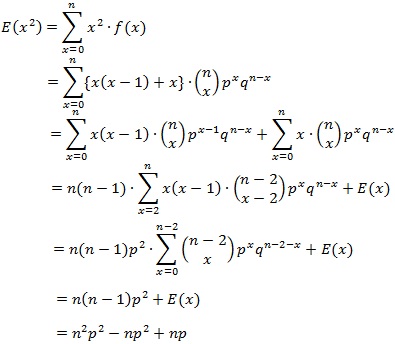
　なので、V(x)は、次の通りです。

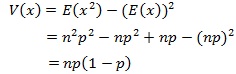
４－２．ポアソン分布

　上記の二項分布は利用範囲は非常に広いですが、試行回数ｎが大きく、発生確率が低いような場合には、ポアソン確率分布（Poisson distribution）が適していると言えます。

　例えば、列車事故などは、列車の通過回数は大量に観察されますが、列車事故の発生確率は非常に小さいものとなっています。「年に３回列車事故が発生する確率は？」といった場合、二項分布による計算は煩雑さが伴います。他にも、大量生産の不良品が見つかる確率などもポアソン確率分布が利用される良例と言えます。

　ポアソン確率分布は、ポアソンの小数の法則（Poisson's law of small numbers）を利用して、ポアソン分布（Poisson distribution）というものを導き出すことができます。

　ポアソン分布は、二項分布の期待値npをある一定数ｍを保ちつつ、ｎ→∞、ｐ→０として二項分布を極限計算して求められるものです。詳細な計算はここでは示しませんが、ポアソン分布は結果として次のような確率分布となります。

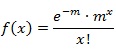
　ポアソン分布の最大の特徴点は、期待値と分散が次のように等しくなることです（計算省略）。

４－３．幾何分布

　幾何分布（geometric distribution）とは、ベルヌーイ試行で、ｘ－１回目までは失敗が続き、ｘ回目で初めて成功した場合のような確率分布のことをいいます。すなわち、次のような分布となります。

　幾何分布における平均と分散は次のようになります。

　幾何分布は、確率変数ｘを時間として考えると、ある事象が初めて発生するまでの待ち時間を表すことになるので、待ち時間分布（waiting time distribution）ということもあります。

４－４．負の二項分布

　幾何分布を少し発展させたものが負の二項分布（negative binomial distribution）です。負の二項分布は、ある事象がX回生じるまでに要する確率を求める場合の確率分布です。前項の幾何分布が「初めてそれが生じるまでの確率」を取り扱っているのに対し、負の二項分布は「所定回数が生じるまでの確率」に関する問題です。

　別の考え方として二項分布と比較した場合、二項分布はベルヌーイ試行の回数が決められているのに対し、負の二項分布は発生事象の回数が決められていると言えます。例えば、コイン投げを考えた場合、二項分布は「コインをｎ回投げて、表がｘ回出る確率分布」であるのに対し、負の二項分布は「コインを投げて表がｘ回出るまでのベルヌーイ試行の回数の確率分布」といえます。

　負の二項分布は次のようになります。ｘ回起きるまでには、ｎ－１回目までにｐがｘ－１回発生し、かつｐでない場合（すなわちｑ）がｎ－ｘ回発生しているはずです。そして、最後にｘ回目（ｎ回目）にｐが発生しているのです。